Oblicz cos kąta XxX: Cześć! Mam taką prośbę może ktoś to rozwiązać Podstawą ostrosłupa prostego ABCS jest trójkąt prostokątny ABC o przyprostokątnych długości AC=6 i BC=8. Wysokość tego ostrosłupa jest równa 12. Oblicz cos kąta nachylenia krawędzi bocznej do płaszczyzny podstawy. Z góry dziękuje za pomoc

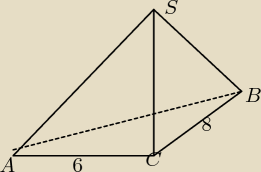Basia: ostrosłup jest prosty czyli CS ⊥ do podstawy (czyli także do AC i BC) czyli CS jest jego wysokością CS = 12 czyli AS² = 6²+SC² BS² = 8²+SC² wylicz a potem

	AC
cos∡CAS =
	AS

	BC
cos∡CBS =
	BS

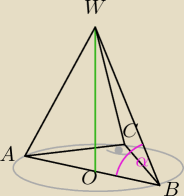dero2005: w ostrosłupie prostym o podstawie trójkąta prostokątnego spodek wysokości wypada w środku przeciwprstokąnej. Liczymy przeciwprostokątną. c = √a² + b² = √6² + 8² = √100 = 10 połowa przeciwprostokątnej |OB| wynosi

	10
|OB| =		= 5
	2

liczymy krawędź boczną |BW| z Pitagorasa |BW| = √OB² + OW² = √5² + 12² = √169 = 13 liczymy cos α

	|OB|		5
cos α =		=
	|BW|		13

M: Czy w ostrosłupie prostym wszystkie krawędzie mają taką samą długość?

M: Mam na myśli krawędzie boczne.

5-latek: Nie bo np jedna sciana moze byc prostopadla do podstawy

misiu: Tak, w ostrosłupie prostym wszystkie krawędzie boczne są równe

sda: αβγδπΩ∞∞∞≤→⇒⇒⇒→→→←←←≠